\[ f(x) = \sum_{k=0}^\infty c_k x^k = c_0 + c_1 x + c_2 x^2 + \dotsb. \]
This is an approximation that is a function of h and derivatives of \(f(x)\) are elements of parameters.
\(f(x \pm h) = f(x) \pm hf'(x) + \frac{h^2}{2}f''(x) \pm \frac{h^3}{6}f'''(x) + O(h^4)\)
Let’s think about \(\sin(x)\).
\[ f(x) = \sin(x) \ f(0) = 0, f'(x)=\cos(x)\ f'(0)=1, f''(x)=-\sin(x)\ f''(0)=0 \]
Thus,
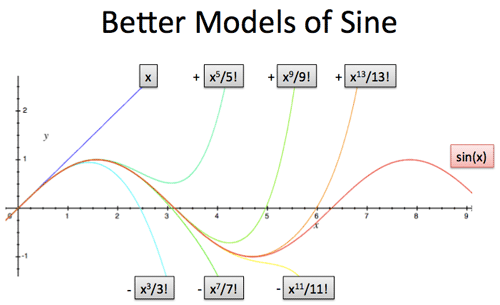
\[\begin{align*} \sin(x) &= 0 + \frac{1}{1!}x + \frac{0}{2!}x^2 + \frac{-1}{3!}x^3 + \dotsb &= x - \frac{x^3}{3!} + \frac{x^5}{5!} - \dotsb, \end{align*}\]
This is approximation. Now \(x\) becomes \(h\) and parameters calculated from derivatives of \(f(x)\) at \(0\).
\(f(x \pm h) = f(x) \pm hf'(x) + \frac{h^2}{2}f''(x) \pm \frac{h^3}{6}f'''(x) + O(h^4)\)
Taylor series and Newton’s bionomial theorem explain the complex exponent.
\[\exp(z) = e^{z}, \ z = a+bi \]
The imaginary exponent is hard to understand intuitively. The exponential function \(e^{x}\) on a complex domain can be regarded as a function exp(x) that behaves like exponential function, i.e. a product of functions is addion of arguments \(\exp(x) \exp(y) = \exp(x+y)\). The product of \(\exp\) fucntion becomes addition of arguments by Newton’s binomical theorem. The costomary expression is \(e^{x}\). This can be done when \(\exp(x) = \Sigma ^{\infty}_{n=0} \frac {Z^{n}}{n!}\) The taylor series with repidly decaying pactorial coefficients \(n!\). This series converges absolutely for every complex \(z\) and converges uniformly on every bounded subset of the complex plain. Rudin’s Real and complex analysis.