A sequence can be defined as a function on the domain of natural number like \(1, 1/2, 1/3 ... 1/n\). This sequence approach to the 0, but never touch the 0. However, people can not take their desire to link the sequence and the 0. Because \(\infty\) is not a member of the natural number even real number, another concept is necessary to link the sequence and the 0. It is the limit. \[ \lim{n\to\infty} \]
The above sequence approach to the 0. But does all sequences approach to some points? What if the sequence is \(1/n\) if \(n\) is not multiple of 100, 0.001 if n is multiple of 100.
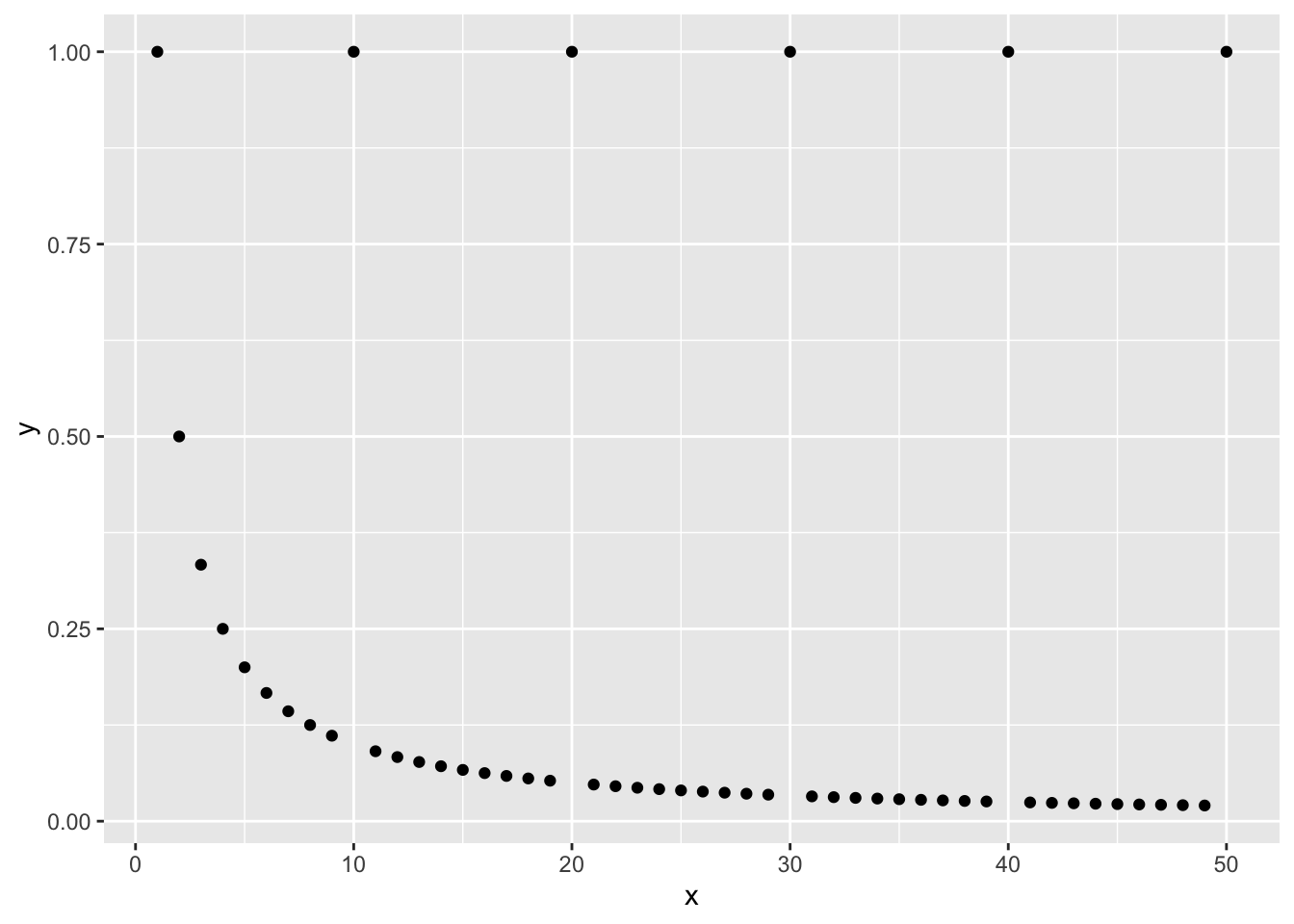
Its approach to zero except at every multiple of 10. The \(\epsilon\) is used for the definition of limit to exclude this example.
The sequence \(S\) is converges the limit \(a\) if for every positive \(\epsilon\), natural number \(N\) is present such that \(\vert a-Sn \vert <\epsilon\) is true in every \(n>N\). Otherwise, the limit is not defined and the sequence is divergent.
In topological space, the \(\epsilon\) becomes the neighborhood.
