Differential equations describe the change of state. The change relates to the state. The solutions of the differential equations are the status equations. The initial conditions set the time \(t\) and status \(y\). The boundary conditions are the value of boundary \(y_0\) and \(y_1\).
\(dy \over dt\) \(= ay + q(t)\) starting from \(y(0)\) at \(t = 0\). inital conditions \(t = 0\) and \(y=1\)
\(q(t)\) is a input and \(y(t)\) is a response. If \(q(t)\) is delta function, the response is said Impulse response \[y' -ay = \delta (t) \\ y(t)=e^{at}\].
The solutions are combination of particular solution and null solution \(y = y_t + y_n\). The solution includes \(e^{at}\). The differential equations can not be solved like polynomial equations, because the arguments of the differential equation relate to each other by calculus in the background of the equation. They can not be treated as just different arguments. The Fourier transformation puts the \(y\) and its derivative \(y'\) in the same functional space (Hilbert space). This transformation makes the differential equation problem to simple arithmetic problem.
Fourier transformation \(F(x) = \Sigma ^{\infty}_{n=-\infty} c_{n}e^{inx}\)
The basis of the Fourier transformation is \(e^{inx}\). If the coefficients of the basis \(c_{n}\) decay fater, \(F(x)\) becomes smooth. If the coefficients are constant, \(F(x)\) is delta function \(\delta(x)\).
The derivative \(dy \over dt\) is an linear transformation operator, i.e. inner product, because the \(y\) and \(y'\) are in functional space with same basis. The defivative can be represented as a matix \(A\). The derivative matrix is antisymetric i.e. \(A^T = -A\) and the minus second derivative matrix \(-d^{2}/dx^{2}\) is symetic positive definite. \(AAf = -A^{T}Af\). The meaning of transverse of a matrix is \((Ax)^{T}y = x^{T}(A^{T}y)\). Dual and inner product
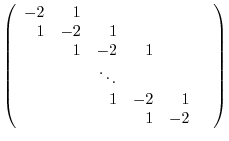
Second difference matrix K
The second difference matrix solves discrete differential equations. The N eigenvectors of K are \(y_{n} = (sin\ n\pi \Delta x, sin\ 2n\pi \Delta x,\ ..., sin\ Nn\pi \Delta x)\). The N eigen values of K are the positive numbers \(\lambda_{n} = 2-2cos {n \pi \over N+1}\).
How does exponent \(i\) mean in \(e^i\)? The exponent makes multiplication to addition. What does an imaginary exponent mean? The imaginary exponent tilts the value to a complex plane. If the base is natural base \(e\), the value of \(e^i\) is in the unit circle of a complex plane. The cycle is \(2 \pi\).
The Fourier transformation for solving the difference equation provoked the subject of functional analysis 200 years ago.
Reference
Differential Equations and Linear Algebra, Gilbert Strang
